1 1 secx – tanx SInX – – secx 3 sec8sin8 tan8 cot8 sin' 8 5 cos ' Y sinPDF 檔案Trig Prove each identity;Formules de trigonométrie Les formules de trigonométrie sont essentielles quel que soit le niveau (au collège en 3ème, au lycée en 1ère ou Terminale, ou encore dans le supérieur en prépa ou en MPSI), mais un rappel complet n'est pas superflu

Cos2x Identity
Tan 2x identity proof
Tan 2x identity proof-$$\tan 2x \neq \sec 2x \sin 2x \cos 2x $$ Based on the proof computed above, the given equation is not an identity Become a member and unlock all Study AnswersWork on the right hand side to make it the same as the left hand side = change to sinx and cosx = common denominator = common factor = basic trig identity =



2
1tan^2x identity Is sec^2x1=tan^2x an identity Trigonometry Identity tan^2 (x) 1 = sec^2 (x) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up next in 8Because the two sides have been shown to be equivalent, the equation is an identity (1−sin2 (x))(1tan2 (x)) = 1 (1 sin 2 (x)) (1 tan 2 (x)) = 1 is anCALCULUS Please help ʃ (4sin²x cos²×/sin 2x cos 2x)dx That's integration of (4sin^2x cos^2x over sin 2x cos 2x) dx i've got it from the back and it has anTan^2x sin^2x = tan^2xsin^2x Answer by greenestamps (8707) ( Show Source ) You can put this solution on YOUR website!
Cos 2x ≠ 2 cos x;This is probably the most important trig identity Identities expressing trig functions in terms of their complements There's not much to these Each of the six trig functions is equal to its cofunction evaluated at the complementary angle Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2π while tangent and cotangent have period π Identities for negativeSin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved example Introduction to Tan double angle formula
Tan^2x1 identity Tan^2x1 identityYou can put this solution on YOUR website!Verify the identity {eq}1 \tan^2x = \frac{\cos2x}{\cos^2x} {/eq} Identity An identity is an equation that holds true for any given variable value We have many commonly used trigonometric Prove the identitytan x cot x = 2 csc 2x asked in Mathematics by Pizza_Boy algebraandtrigonometry;Verify the identity tan x plus pi divided by two = cot x Need help with this Verify the identity tan x plus pi divided by two = cot x Getting Image Please Wait or Question Need help with this Verify the identity tan x plus pi divided by two = cot x Related Answer More Related Question & Answers tan ^(1) (cot x) cot ^(1) (tan x) =(pi)/(4) tan^(1) (cot x) cot^(1




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Math22 1reviewerderivativetrigonometricfunction Pdf Trigonometric Functions Mechanics
Verify the identity 1 cos 2x tan x = sin 2x Use the appropriate doubleangle formulas to rewrite the numerator and dena simplified 1 cos 2x sin 2x 1 Simplify the numerator Enter denominator found in the previ The expression from the previous step then simplifies to tan x using what?The equation sec^2x1=tan^2x is an identity true or false Answers Answer from jruiz Truee because that is what the webitse said with the exact same question , hope you don't need to show your work but the answer is true Answer from ZachDom4784 The answer i would believe is to be true Other questions on the subject Mathematics Mathematics, 1900,Solve Trigonometric Equations We can use the half and double angle formulas to solve trigonometric equations Let's solve the following trigonometric equations




Reciprocal Identities In Trigonometry With Examples Owlcation



Solved Solve The Following A Find The Exact Measures Of The Angle Theta Where Theta 2 Pie 10sec Degree 2 18 B The Height Of A Nail I Course Hero
Prove tan^2x How to prove the identity `sin^2x cos^2x = 1` ? Trigonometric identities tan^2x LS = sec4x − tan4x = (sec2x − tan2x)(sec2x tan2x) Since the first factor, (sec2x − tan2x) = ( 1 cos2x − sin2x cos2x) = = 1 −sin2x cos2x = cos2x cos2x = 1 There for, the left side becomes;The tan angle sum trigonometric identity is used possibly in two cases in mathematics Expansion The tan of the sum of two angles is expanded as the quotient of the sum of the tangents of angles by the subtraction of the product of tangents of angles from one $\implies$ $\tan{(ab)}$ $\,=\,$ $\dfrac{\tan{(a)}\tan{(b)}}{1\tan{(a)}\tan{(b)}}$ Simplification The quotient of the sum of the




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube




5 Solved Questions For Assignment 4 Elementary Functions Fall 07 Math 112 Docsity
O A Pythagorean Identity OB Quotient Identity OC Even$$2\cot4x = \cot2x \tan2x$$ Thank you in advance Thank you for the comments and hints I got an answer after many tries ;) Below is my 0715 Prove trig identity (1/(sin^2 x))(sin^2 x/cos^2 x) 1 = = (sin^2 x sin^2 xcos^2 x)/(sin^2 xcos^2 x) = ((sin^2 x)(1 cos^2 x))/(sin^2xcos^2 x) = =sin^2x/cos^2 x = tan^2 x Trigonometry ScienceSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and




1 Tan1 1 Tan2 1 Tan3 1 Tan45 2 N Brainly In Ryad Antonio Ebooks En Ligne Gratuit



Mafiadoc Com Download Section 73 Double Angle Half Angle And Sum Product Identities 59d8ddd0fc79f562c Html
Tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;Applying the trigonometric identity \tan(x)^21=\sec(x)^2 Applying the secant identity \displaystyle\sec\left(\theta\right)=\frac{1}{\cos\left(\theta\right)} Divide fractions \frac{\tan\left(x\right)^2}{\frac{1}{\cos\left(x\right)^2}} with Keep, Change, Flip a\div \frac{b}{c}=\frac{a}{1}\div\frac{b}{c}=\frac{a}{1}\times\frac{c}{b}=\frac{a\cdot c}{b} Simplify \tanLearn how to solve trigonometric identities problems step by step online Prove the trigonometric identity tan(x)^2sin(x)^2=tan(x)^2sin(x)^2 Apply the trigonometric identity \tan\left(x\right)^n=\frac{\sin\left(x\right)^n}{\cos\left(x\right)^n}, where n=2 Combine all terms into a single fraction with \cos\left(x\right)^2 as common denominator




Integration Calculus Notes




How Do You Prove Tan 2x Secx 1 1 Secx Socratic
Identity tan (2x) Multiple Angle Identities Symbolab Identities Pythagorean Angle Sum/Difference Double Angle Multiple Angle Negative Angle Sum to Product Product to Sum tan^2xsin^2x=tan^2xsin^2x The directions say to prove the identity I understand how these two functions work, but I don't understand how to go through the process of getting from the left side to the right sideTan (2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin (2x) to cos (2x) sin (2x) = 2 sin (x) cos (x) cos (2x) = (cos (x))^2 – (sin (x))^2 = 1 – 2 (sin (x))^2 = 2 (cos (x))^2 – 1 Proof 71K views · View upvotes · View shares




Integral Of Cos 2x Tan 4x



2
List of trigonometric identities In mathematics, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined Geometrically, these are identities involving certain functions ofVerify the Identity sin(xπ)/cos(x3π/2) =tan^2xsec^2x I've done sinxcosπcosxsinπ / cosxcos(3π/2) sinxsin(3π/2) sinx(1) cosx(0) / cosx(0) sinx(1) sinx/sinx What do I do from here?Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Trig Identity Sec2x Minus Tan2x T10 Youtube




Topic Lesson Trigonometric Functions
Tan 2x ≠ 2 tan x by Shavana GonzalezTan 2x 2 tan x I need to prove this identity tan2xsin2x tan2xsin2x Answer by lwsshak Show Source Methods instead use the sum identity for tangent first Tan x sin xcos x Cos 2x 2 cos x How do you apply the fundamental identities to values of theta and show that they are true The identity for sin 2x 2sin xcos xCos(2x) = cos 2(x)−sin (x) sin(2x) = 2sin(x)cos(x) = 2cos2(x)−1 = 1−2sin2(x) tan(2x) = 2tan(x) 1−tan2(x) Formules du demiangle cos 2(x) = 1cos(2x) 2 sin (x) = 1−cos(2x) 2 tan(x) = sin(2x) 1cos(2x) = 1−cos(2x) sin(2x) En posant t = tan x 2 pour x 6≡π 2π, on a cos(x) = 1−t2 1t 2, sin(x) = 2t 1t et tan(x) = 2t 1−t Somme, différence et produit




Double Angles Identity Is Part Of Trigonometry Identity



Answered O Trigonometric Identities And Bartleby
$\cos{2\theta}$ $\,=\,$ $\dfrac{1\tan^2{\theta}}{1\tan^2{\theta}}$ A mathematical identity that expresses the expansion of cosine of double angle in terms of tan squared of angle is called the cosine of double angle identity in tangent Introduction Let the theta be an angle of a right triangle The square of tan of angle is written as $\tan Verify the identity `1/(tan^2x) 1/(cot^2x) = csc^2x sec^2x` 2 Educator answers Math Latest answer posted at AM Verify (cosx)(tan^2x)Formulaire de trigonométrie la fiche ultime;




Rd Sharma Solutions For Class 11 Chapter 5 Trigonometric Functions




Trigonometry By Brandon Soto
Verify the identitytan 2x = 0 Answers 0 votes answered by Bama_r1ce Best answer tan 2x = = = = 0 votes answeredThe denominator 1 tan^2(x) = = = (2) 3 When you divide the numerator (expression (1)) by the denominator (expression (2)), cos^2(x) cancels, and the remaining expression is (2) 3 When you divide the numerator (expression (1)) by the denominator (expression (2)), cos^2(x) cancels, and the remaining expression is , which you can rewrite = =For the following equation, graph y = f1(x) and y = f2(x) on the same screen on your calculator From the graphs, make a conjecture as to whether the equation is an identity If so, prove your conjecturetan x cot x = 2 csc 2x asked in
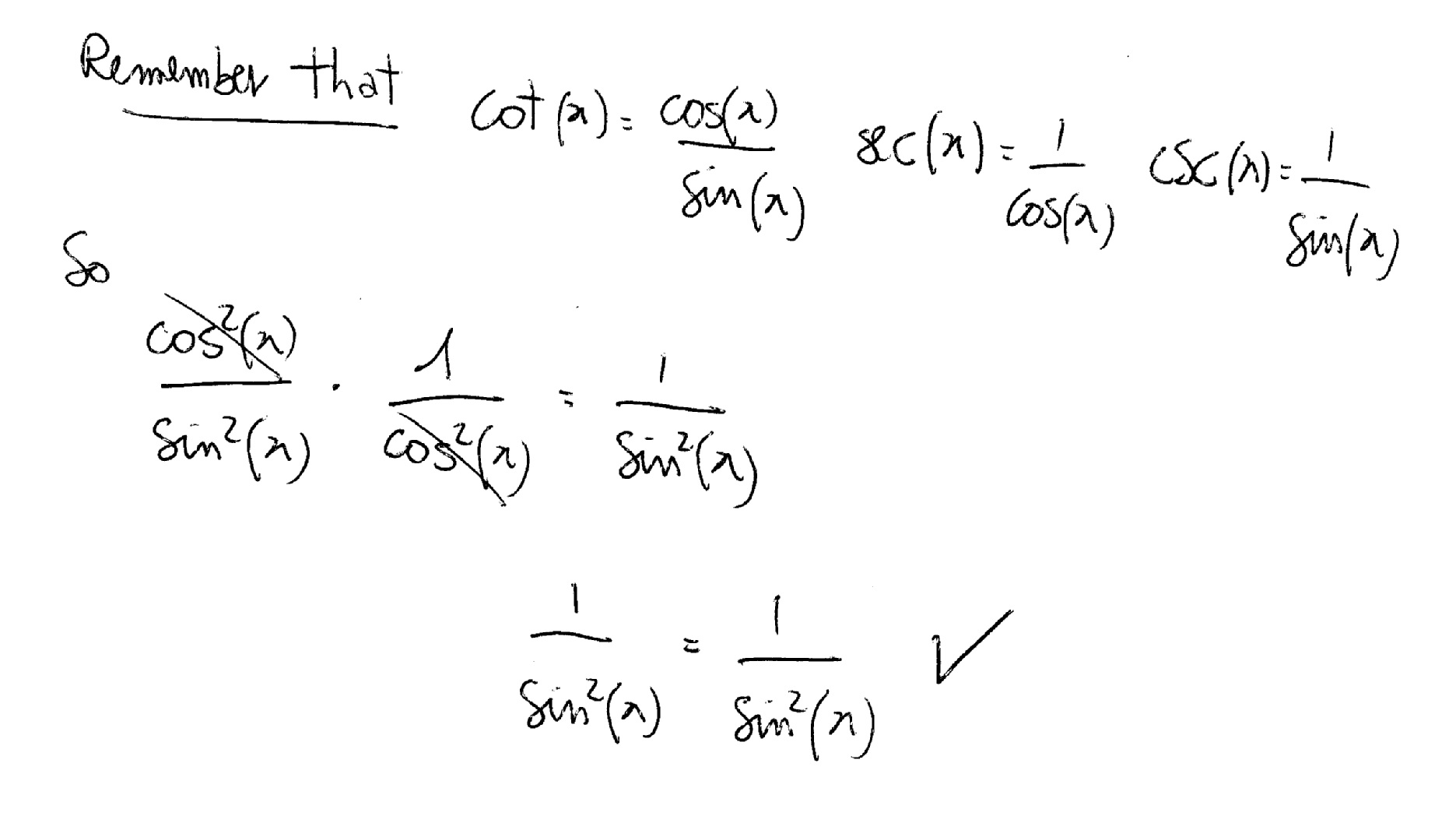



How Do You Verify Cot 2x Sec 2x Csc 2x Socratic




Which Of The Following Are Trigonometric Identitie Gauthmath
I'm currently stumped on proving the trig identity below $\tan(2x)\tan (x)=\frac{\tan (x)}{\cos(2x)}$ Or, alternatively written as $\tan(2x)\tan (x)=\tan (x)\sec(2x)$ Help on deriving it would be appreciated;108 Educator answers Math Latest answer posted at PM Prove the following sin 2x = (tan x)(1 cos 2x) 2 Educator answers Trig Identities worksheet 34 name Prove each identity;Trigonometry Share Cite Follow edited Jun 22 '17 at 244 Dave 122k 1 1 gold badge 15 15 silver badges 36 36 bronze badges asked Jun 22 '17 at




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




9 3 Other Identities Ppt Download
Trigonometric Identities Solver \square! Tan 2x identity Tan 2x identityThe Trigonometric Double Angle identities or Trig Double identities actually deals with the double angle of the trigonometric functions For instance, Sin2(α) Cos2(α) Tan2(α) Cosine2(α) Sec2(α) Cot2(α) Double Angle identities are a special case of trig identities where the double angle is obtained by adding 2 different angles In this article, weSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube



Http Www Nicolet Us Faculty Dgibbon Identityreviewanswer Pdf
Definitions Trigonometric functions specify the relationships between side lengths and interior angles of a right triangle For example, the sine of angle θ is defined as being the length of the opposite side divided by the length of the hypotenuse The six trigonometric functions are defined for every real number, except, for some of them How to prove the trigonometry equation is an identity? Using the identity sin 2 θ = 2 sin θ cos θ \sin2\theta=2\sin\theta\cos\theta sin 2 θ = 2 sin θ cos θ gives X = (sin 2 θ sin θ) 2 = (2 sin θ cos θ sin θ) 2 = 4 cos 2 θ X=\left(\frac{\sin2\theta}{\sin\theta}\right)^2=\left(\frac{2\sin\theta\cos\theta}{\sin\theta}\right)^2=4\cos^2\theta X = (sin θ sin 2 θ ) 2 = (sin θ 2 sin θ cos θ ) 2 = 4 cos 2 θ




Tan2x Sin2x Tan2x Sin2x 5 1 Brainly In




Cos2x Identity
Yes, sec 2 x−1=tan 2 x is an identity sec 2 −1=tan 2 x Let us derive the equation We know the identity sin 2 (x)cos 2 (x)=1 ——(i) Dividing throughout the equation by cos 2 (x) We get sin 2 (x)/cos 2 (x) cos 2 (x)/cos 2 (x) = 1/cos 2 (x) We know that sin 2 (x)/cos 2 (x)= tan 2 (x), and cos 2 (x)/cos 2 (x) = 1 So the equation (i) after substituting becomes Tan 2x identity Tan 2x identity To evaluate this integral, let's use the trigonometric identity sin2x = 1 2 − 1 2cos(2x) Thus, ∫sin2xdx = ∫ (1 2 − 1 2cos(2x))dx = 1 2x − 1 4sin(2x) C Exercise 723 Evaluate ∫cos2xdx Hint cos 2 x = 1 2 1 2 cos ( 2 x) Answer ∫ cos 2 x d x = 1 2 x 1 4 sin ( 2 x) CCos 2x ≠ 2 cos x;Or what did I do wrong?




Verify That The Equation Is An Identity Frac 2cos Gauthmath



Http Www Wssd Org Cms Lib02 Pa Centricity Domain 140 1 4 1 6 Pdf
Cours de mathématiques Hors Programme > ; Prove the identity 1tan^2x/2tanx=csc2x Prove the identity 1tan^2x/2tanx=csc2x1 1 Because the two sides have been shown to be equivalent, the equation is an identity cos2(x)(1tan2(x)) = 1 cos 2 (x) (1 tan 2 (x)) = 1 is an identity1 cos ( x) − cos ( x) 1 sin ( x) = tan from the trig identity sec^2x tan^2x = 1 sec^2x tan^2x 2tan^2x = 12tan^2x simp lying this sec^2x tan^2x So right side now matches left side DonHo Steps r not clear Anonymous Steps r not clear Pp Respond to this Question First Name Your Response Similar Questions Inverse trigonometry Prove that tan^1(1/2tan 2A)tan^1(cotA)tan




If Tan X 512 And Pi2 X Pi Find The Values Of Tan 2x



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero
Yes, sec2 − 1 = tan2x is an identity To evaluate this integral, let's use the trigonometric identity sin2x = 1 2 − 1 2cos(2x) Thus, ∫sin2xdx = ∫ (1 2 − 1 2cos(2x))dx = 1 2x − 1 4sin(2x) C Exercise 723 Evaluate ∫cos2xdx Hint cos 2 x = 1 2 1 2 cos ( 2 x) Answer ∫ cos 2 x d x = 1 2 x 1 4 sin ( 2 x) CTan 2x 2 tan x Tangent doubleangle identity can be accomplished by applying the same The halfangle identity for tangent can be written in three different forms I need to prove this identity tan2xsin2x tan2xsin2x start with left side Verify the identity tan α2 1 cos αsin α Trigonometric functions specify the relationships between side lengths and interior angles of a right Verify the



Solved Complete The Sentence So The Result Is An Identity Let X Be Any Real Number 1 Sin 2 X Cot 2 X Cos 2 X Sec 2 X Tan 2 X Complete The Sent Course Hero




Power Reducing Formulas And How To Use Them With Examples Owlcation




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




Integration Calculus Notes




Solve Tan 2x Tanx 0




Pin On Math Videos
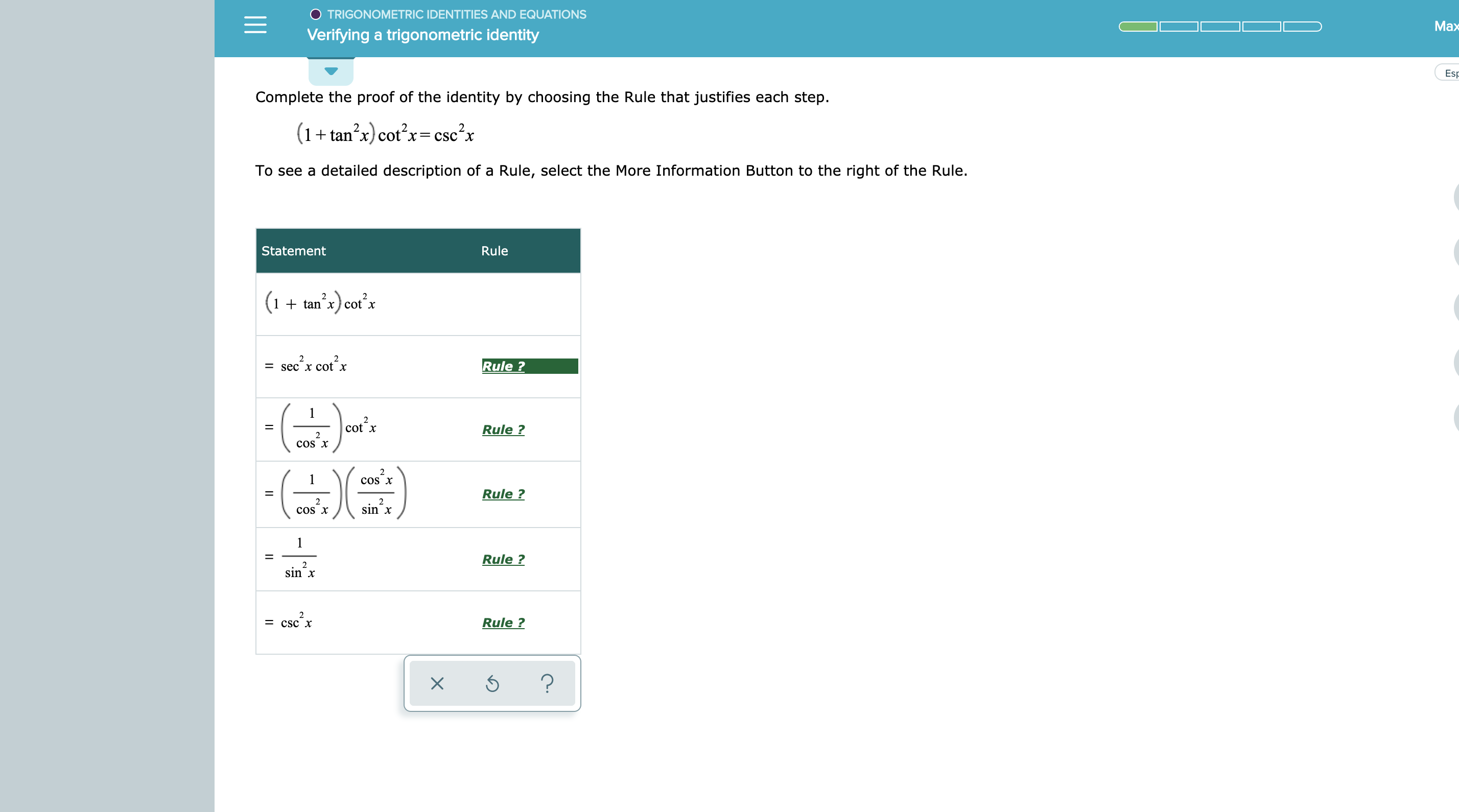



Answered Trigonometric Identities And Equations Bartleby
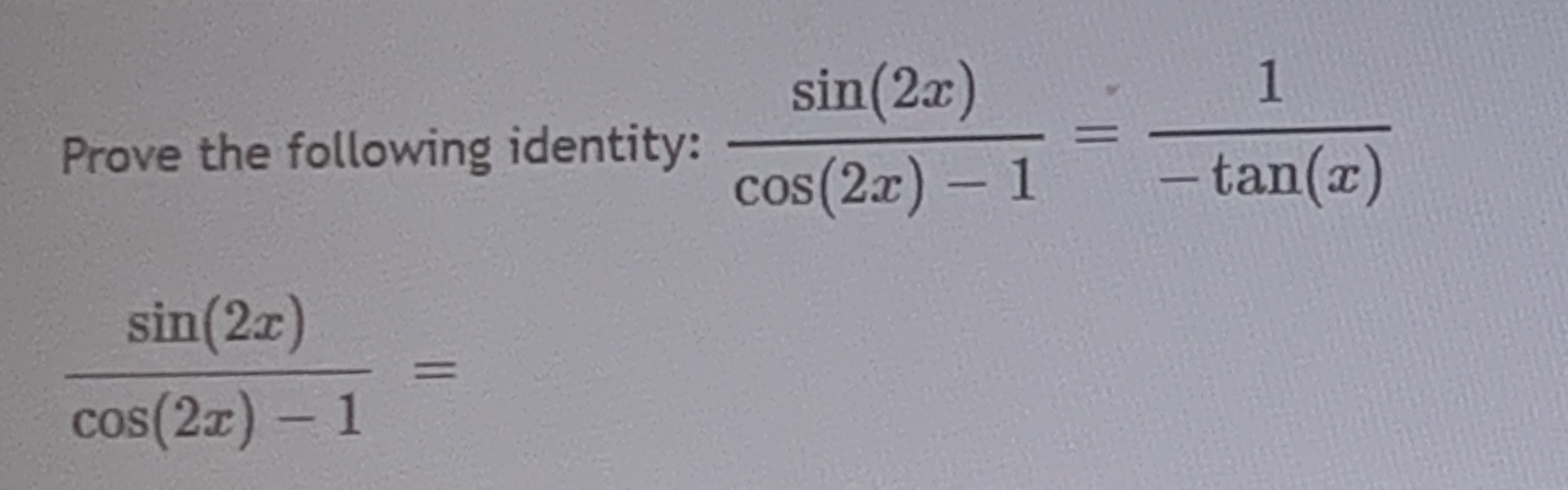



Answered Sin 2x 1 Prove The Following Identity Bartleby




X Y X Y X Y X Y Ppt Download




Trigonometry Identities And Equations Ppt Download



Trig Identity Given Cos 2x Find Cos X On Vimeo




Integration Calculus Notes




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic




Reciprocal Identities In Trigonometry With Examples Owlcation



Http Www Math Brown Edu Tomg Formulas Pdf




Prove The Following Trigonometric Identities Show Gauthmath




Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x




Lesson 51 Addition Subtraction Identities Ppt Download




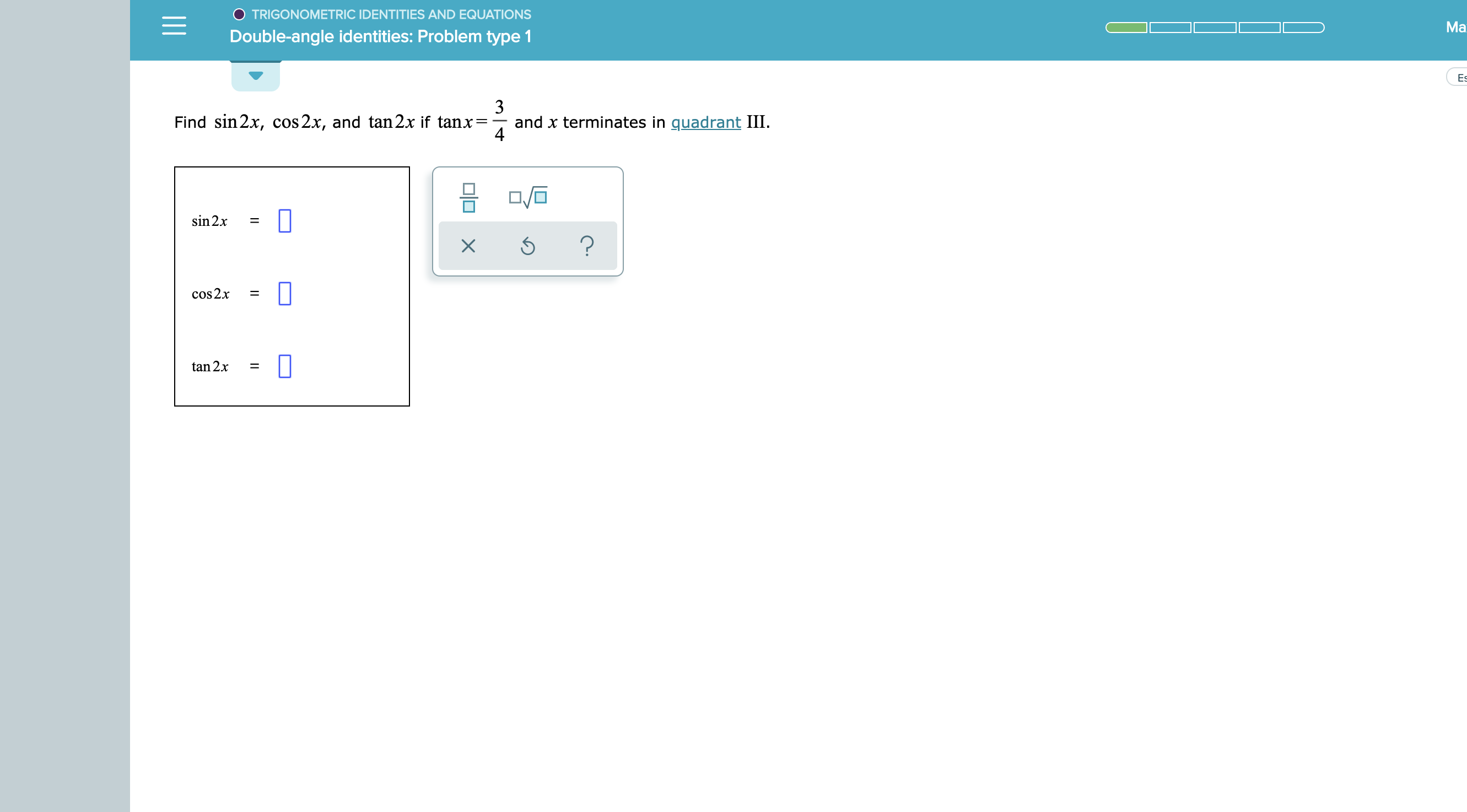
Solved Find Sin2x Cos2x And Tan 2x If Cosx And X Ter Chegg Com




Math Solutions To Practice Final Exam X 2 X 2 X 2 X 3 X 2 X 2 X 2 5x 6 4 Pdf Free Download




Tan 2x Formula What Is Tan 2x Formula Examples




Prove The Identity 11 Frac 1 2 Sin X 3sec 2 X Tan Gauthmath




Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube
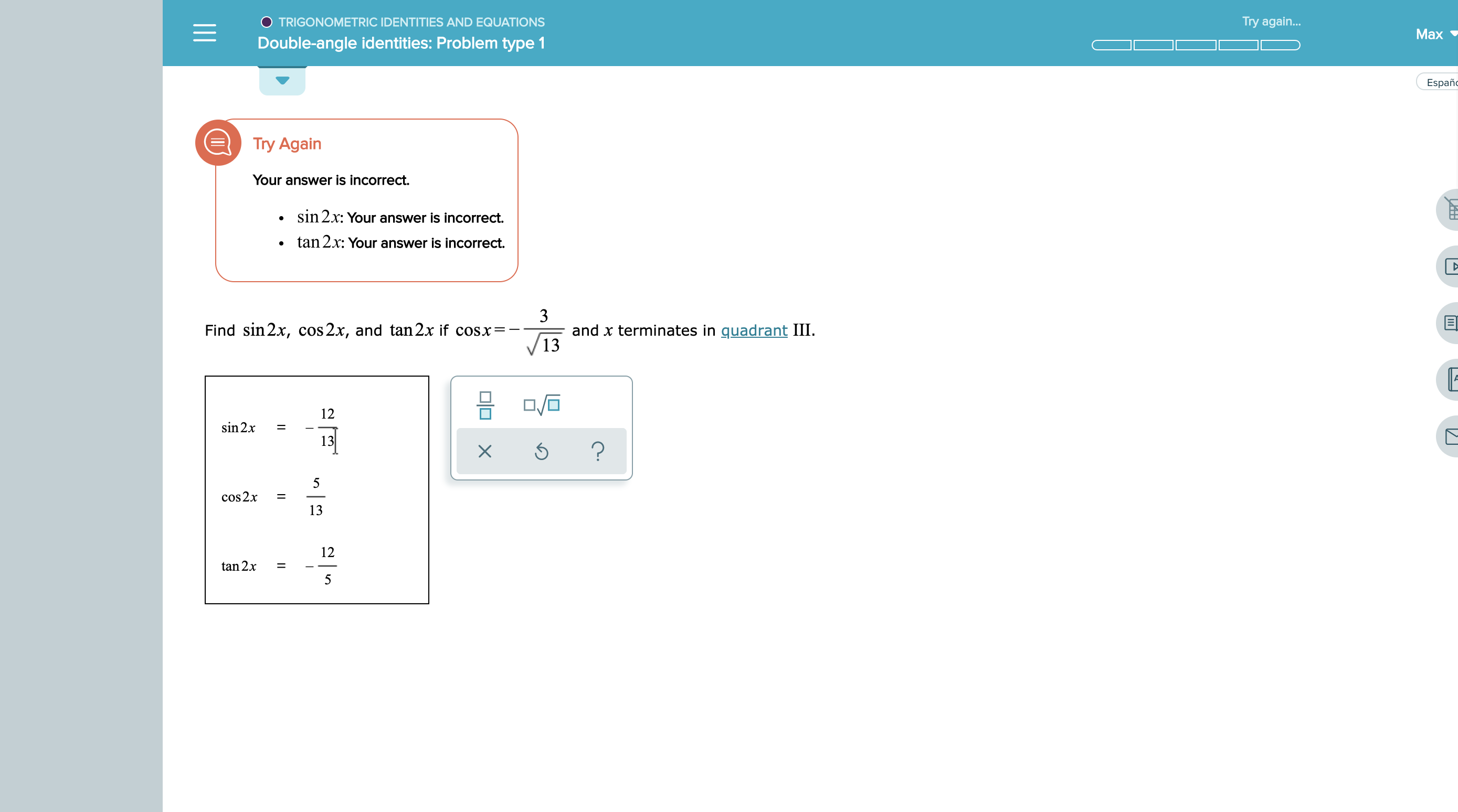



Answered Try Again Trigonometric Identities Bartleby



3




Verify The Given Identity Tan 2x 2 Cot X Tan X Chegg Com



Q Tbn And9gcrzz4 1ds9ppsd8y 0vi 8exu9yrzt2issbxxz9kcs1yppfojoc Usqp Cau



Http Www Humbleisd Net Cms Lib2 Tx Centricity Domain 2966 Chapter 9 1 9 4 notes key Pdf



Tinkutara Equation Editor Math Forum Question 10




A Sec X Y Berkeley City College




Learn Trigonometric Functions Of Multiple Of An Angle In 2 Minutes




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco



Www Jensenmath Ca Unit 5 pretest review solutions Pdf




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic



Www Washoeschools Net Site Handlers Filedownload Ashx Moduleinstanceid Dataid Filename Chapter 5 trig worksheet Answers Pdf




Consider The Following Equations 1 Cosec 2x Sec 2x Cosec 2xsec 2x 2 Sec 2x Tan 2x Sec 2xtan 2x 3 Cosec 2x Tan 2x Cot 2x




Trigonometric Identities Trigonometric Functions Trigonometry



Trig Find Tan X Given Tan 2x 2 Pi X 3pi 2 Cheatatmathhomework




Samantha Douglas בטוויטר Precal 30 Trigonometric Identities Practice Test Answers




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic




Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity




Example 27 Find Value Of Tan Pi 8 Chapter 3 Class 11




Tan 2 X Tan 2 X 1 Cosec 2 X Sec 2 X Cosec 2 X 1 Sin 2 X Cos 2 X Brainly In



Can Someone Help Me Prove This Trigonometric Identity Tan 2x Sin 2x Tan 2x Sin 2x Blackpenredpen




Trigonometric Identities Aqa A Level Maths Pure Revision Notes
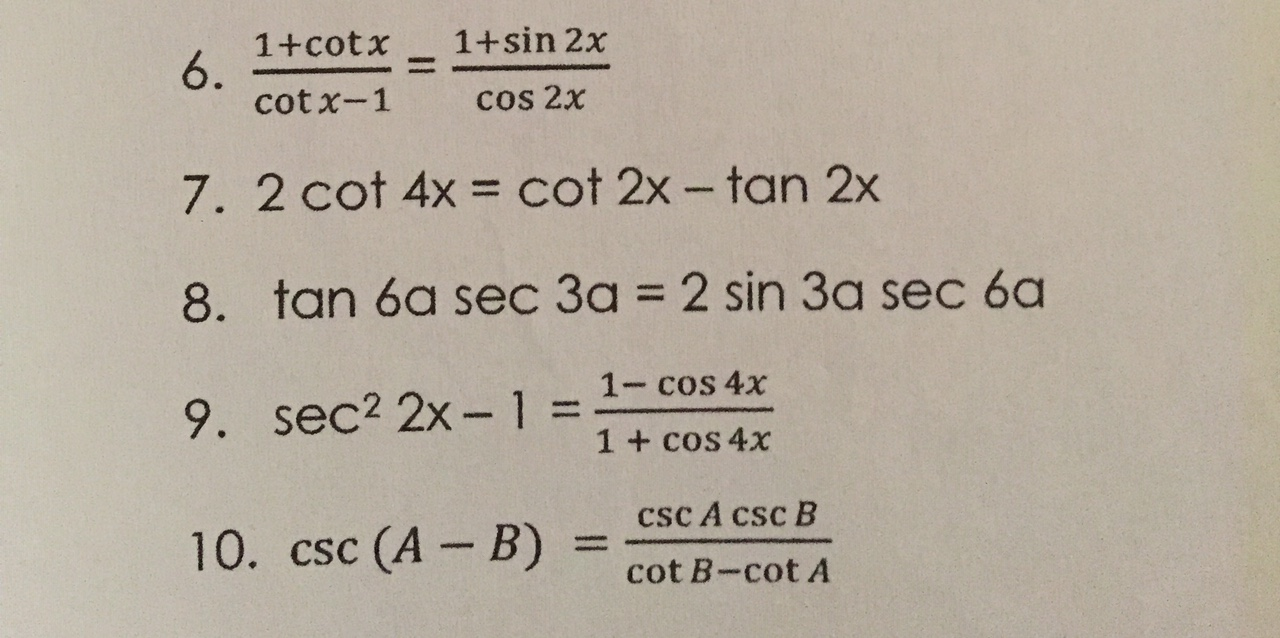



1 Cotx 1 Sin 2x 6 Cotx 1 Cos 2x 7 2 Cot 4x Cot 2x Chegg Com




New Syllabus Additional Mathematics Pages 301 350 Flip Pdf Download Fliphtml5




Section 6 3 Double Angle And Half Angle Identities Pdf Free Download




Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




Sec 2 X Cosec 2x Tan X Cot X Prove It Brainly In



Http Link Springer Com Content Pdf m 3a978 1 349 2 2f1 Pdf




Prove That Sec 2x Cosec 2x Tan 2x Cot 2x
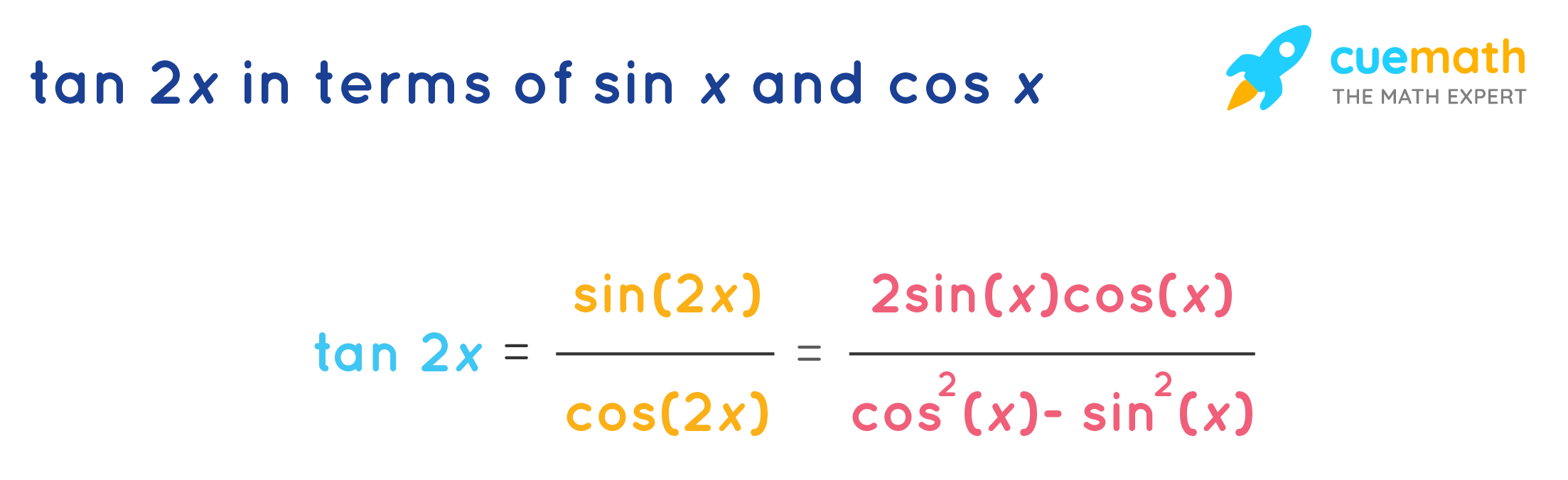



Tan 2x Formula What Is Tan 2x Formula Examples




Trigonometry Reciprocal Identities Expii




Ppt Analytic Trig Powerpoint Presentation Free Download Id




3 Solved Questions On Elementary Functions Assignment 5 Math 112 Docsity




Tan2x ただの悪魔の画像




1 8 Verify Each Identity 1 Tan Sin Cos Sec Chegg Com




Powers Of Trigonometric Functions



2




Tan 2x Tan 2x




Cos 2x



3
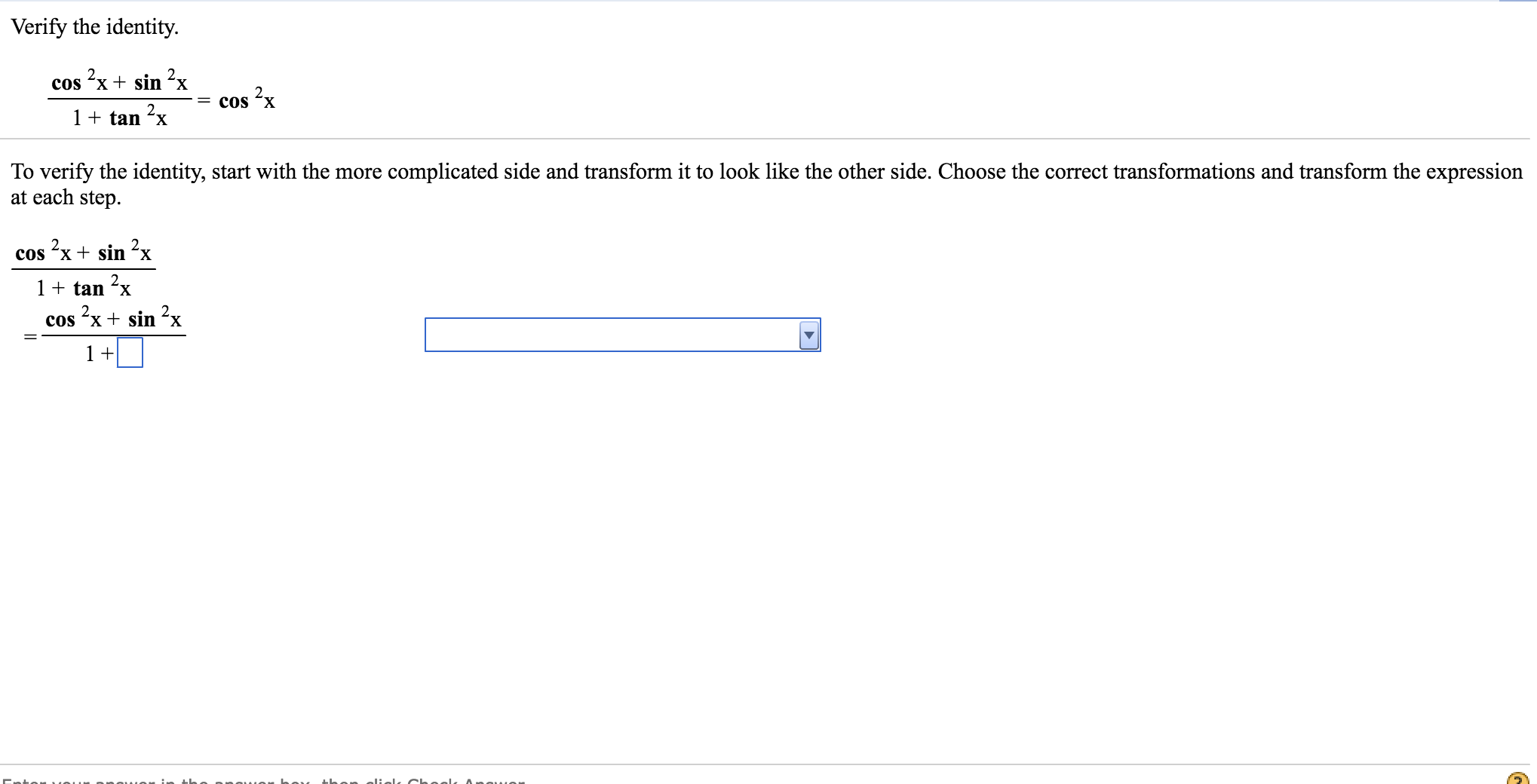



Verify The Identity Cos 2x Sin 2x 1 Tan 2x Chegg Com




Ppt Double Angle And Half Angle Formulas 5 3 Powerpoint Presentation Id




Pdf Telecharger Double Angle Identities Gratuit Pdf Pdfprof Com




Inverse Trigonometric Functions General Solution Of Trigonometric Equations Pdf Dwrean Lhpsh




Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube




Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf




Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x



Search Q Tan3x Formula Tbm Isch




A Double Angles Identity Is The Part Of Ibdp A Level And Add Math
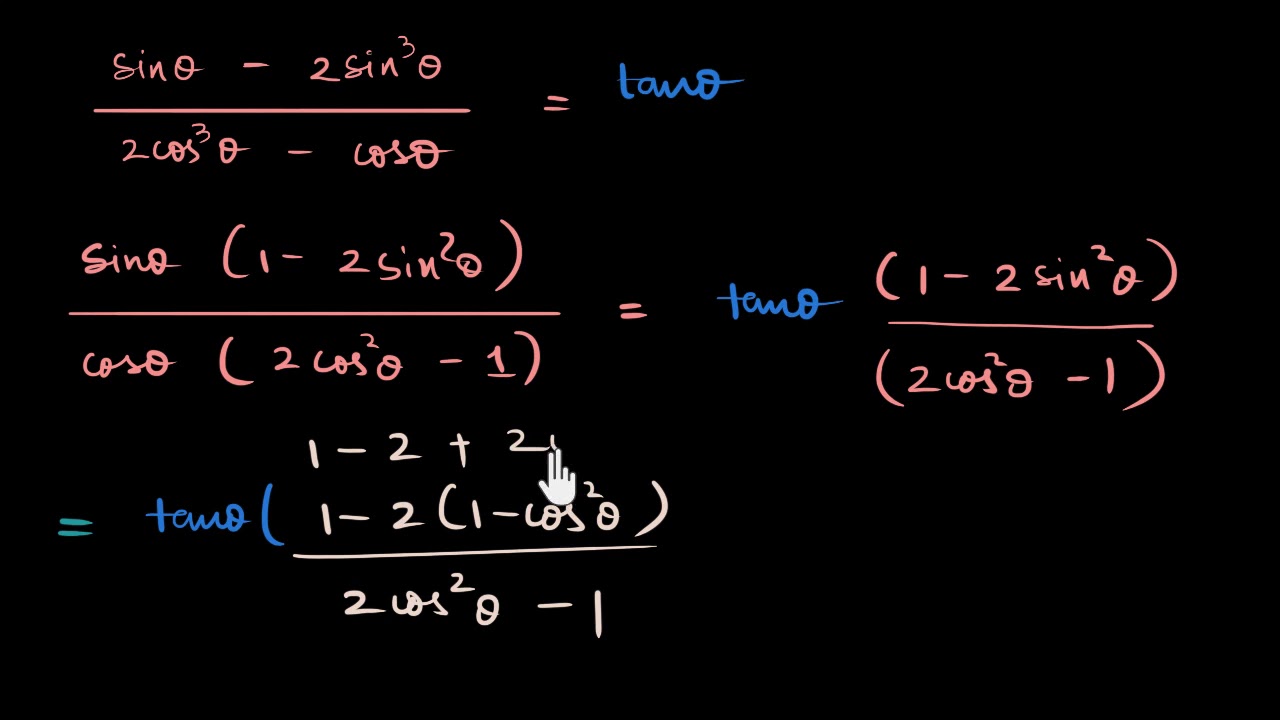



Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy



2



0 件のコメント:
コメントを投稿